2025.02.07 - [Computer Science/자료구조 & 알고리즘] - [자료구조 & 알고리즘] 이진 검색 트리 (feat. 트리)
균형 이진 트리(Balanced Binary Tree)란?
균형 이진 트리(Balanced Binary Tree)는 이진 트리(Binary Tree)의 한 종류로, 트리의 높이를 일정하게 유지하여 탐색, 삽입, 삭제 연산의 시간 복잡도를 O(log n)으로 보장하는 자료구조입니다. 이진 검색 트리(Binary Search Tree, BST)는 트리가 한쪽으로 치우칠 경우 탐색 시간이 O(n)까지 증가할 수 있기 때문에, 이를 해결하기 위해 균형을 유지하는 트리가 필요합니다.
대표적인 균형 이진 트리에는 AVL 트리와 레드-블랙 트리가 있습니다.
이번에는 AVL 트리에 대해 학습할까 합니다.
AVL 트리란?
AVL 트리는 균형 이진 검색 트리(Balanced Binary Search Tree)의 일종으로, 트리의 높이 균형(Balance)을 유지하여 탐색(Search), 삽입(Insertion), 삭제(Deletion) 연산의 시간 복잡도를 **O(log n)**으로 보장하는 자료구조입니다. AVL 트리는 이진 검색 트리가 한쪽으로 치우치면서 발생할 수 있는 성능 저하를 해결하기 위해 설계되었습니다.
AVL 트리는 1962년 Adelson-Velsky와 Landis가 개발했으며, 이름은 개발자의 이니셜에서 따왔습니다.
1. AVL 트리의 특징
1.1 균형 인수(Balance Factor)
AVL 트리는 각 노드에서 균형 인수(Balance Factor, BF)가 -1, 0, 1 사이로 유지되도록 설계되었습니다.
균형 인수는 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이를 의미하며, 아래와 같이 정의됩니다.
BF(node)=높이(왼쪽 서브트리)−높이(오른쪽 서브트리)
1.2 균형 상태와 불균형 상태
균형 상태 예시
30
/ \
20 40
/ \
10 50
각 노드의 균형 인수:
- 노드 30: BF = 높이(왼쪽 서브트리) - 높이(오른쪽 서브트리) = 2 - 2 = 0
- 노드 20: BF = 1 - 0 = 1
- 노드 40: BF = 0 - 1 = -1
모든 노드의 균형 인수가 -1, 0, 1 사이에 있으므로 균형 상태입니다.
불균형 상태 예시
1) 왼쪽 불균형 (LL 케이스)
30
/
20
/
10
- 노드 30의 BF = 2 - 0 = 2로 불균형 상태입니다.
2) 오른쪽 불균형 (RR 케이스)
10
\
20
\
30
- 노드 10의 BF = 0 - 2 = -2로 불균형 상태입니다.
2. AVL 트리의 주요 연산
2.1 탐색(Search)
탐색 연산은 일반적인 이진 검색 트리와 동일하게 수행됩니다.
현재 노드의 키 값과 찾고자 하는 키 값을 비교하여 왼쪽 또는 오른쪽 서브트리로 이동하며 진행합니다.
탐색 알고리즘 (Python)
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
def search(node, key):
if node is None or node.key == key:
return node
if key < node.key:
return search(node.left, key)
else:
return search(node.right, key)
탐색 예시
트리에서 키 50을 탐색한다고 가정합니다.
30
/ \
20 40
\
50
- 루트 노드 30에서 시작합니다. 50 > 30이므로 오른쪽 서브트리로 이동합니다.
- 노드 40에서 50 > 40이므로 오른쪽 서브트리로 이동합니다.
- 노드 50에서 탐색이 완료됩니다.
탐색 결과: 노드 50을 찾았습니다.
2.2 삽입(Insertion)
AVL 트리에 노드를 삽입하면 균형 상태가 깨질 수 있습니다.
삽입 후 균형 인수를 계산하고 불균형 상태일 경우 회전(Rotation) 연산을 통해 복구합니다.
삽입 알고리즘 (Python)
def insert(node, key):
if node is None:
return Node(key)
if key < node.key:
node.left = insert(node.left, key)
else:
node.right = insert(node.right, key)
# 노드 높이 업데이트
node.height = 1 + max(get_height(node.left), get_height(node.right))
# 균형 인수 계산
balance = get_balance(node)
# 불균형 상태에 따른 회전 연산
if balance > 1 and key < node.left.key: # LL 회전
return rotate_right(node)
if balance < -1 and key > node.right.key: # RR 회전
return rotate_left(node)
if balance > 1 and key > node.left.key: # LR 회전
node.left = rotate_left(node.left)
return rotate_right(node)
if balance < -1 and key < node.right.key: # RL 회전
node.right = rotate_right(node.right)
return rotate_left(node)
return node
2.3 삭제(Deletion)
AVL 트리에서 노드를 삭제하면 마찬가지로 균형 상태가 깨질 수 있습니다.
삭제 후 균형 인수를 계산하여 필요 시 회전 연산을 수행합니다.
삭제 알고리즘 (Python)
def delete(node, key):
if node is None:
return node
if key < node.key:
node.left = delete(node.left, key)
elif key > node.key:
node.right = delete(node.right, key)
else:
if node.left is None:
return node.right
elif node.right is None:
return node.left
temp = min_value_node(node.right)
node.key = temp.key
node.right = delete(node.right, temp.key)
# 높이 및 균형 인수 업데이트
node.height = 1 + max(get_height(node.left), get_height(node.right))
balance = get_balance(node)
# 불균형 상태에 따른 회전 연산
if balance > 1 and get_balance(node.left) >= 0:
return rotate_right(node)
if balance > 1 and get_balance(node.left) < 0:
node.left = rotate_left(node.left)
return rotate_right(node)
if balance < -1 and get_balance(node.right) <= 0:
return rotate_left(node)
if balance < -1 and get_balance(node.right) > 0:
node.right = rotate_right(node.right)
return rotate_left(node)
return node
3. 회전 연산 (Rotation)
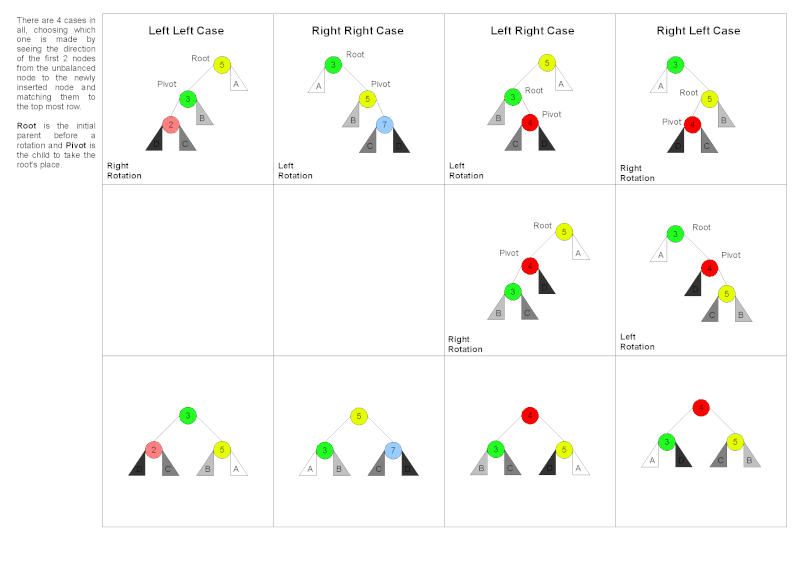
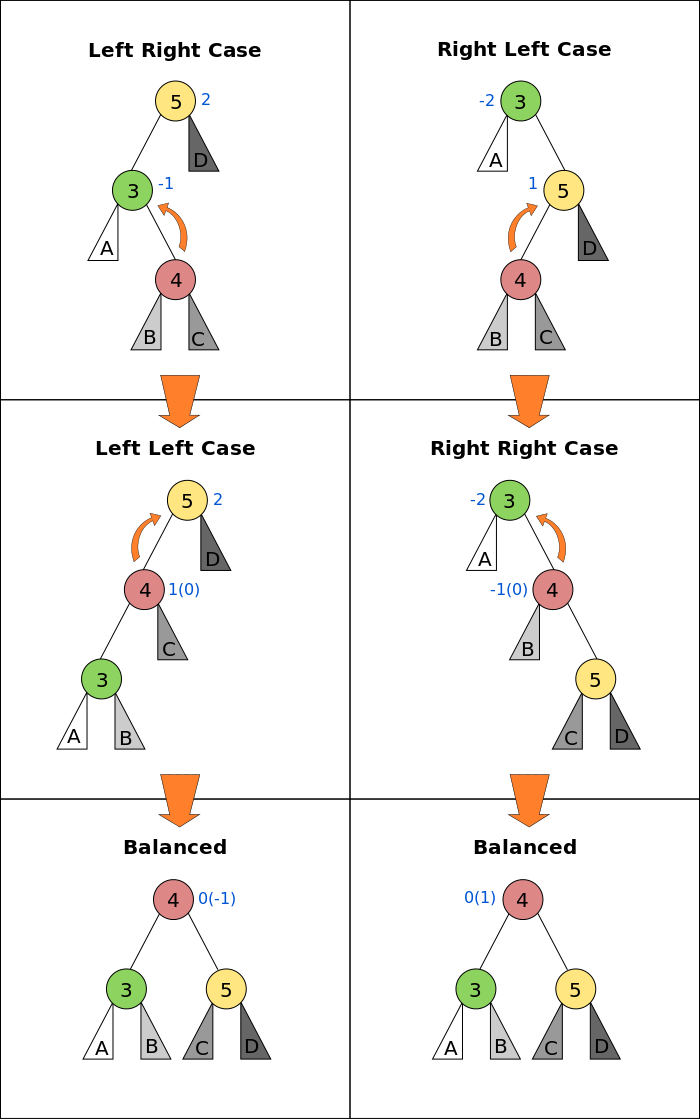
회전 연산에는 다음과 같은 네 가지 종류가 있습니다.
- LL 회전: 왼쪽 자식의 왼쪽 서브트리에서 불균형 발생 → 오른쪽 회전
- RR 회전: 오른쪽 자식의 오른쪽 서브트리에서 불균형 발생 → 왼쪽 회전
- LR 회전: 왼쪽 자식의 오른쪽 서브트리에서 불균형 발생 → 왼쪽-오른쪽 회전
- RL 회전: 오른쪽 자식의 왼쪽 서브트리에서 불균형 발생 → 오른쪽-왼쪽 회전
4. AVL 트리의 시간 복잡도
AVL 트리는 항상 트리의 높이를 O(log n)으로 유지하기 때문에 탐색, 삽입, 삭제 연산 모두 최악의 경우에도 O(log n) 시간 복잡도를 가집니다.
연산 시간 복잡도
| 탐색(Search) | O(log n) |
| 삽입(Insertion) | O(log n) |
| 삭제(Deletion) | O(log n) |
5. AVL 트리의 활용 예시
- 데이터베이스 인덱스: 빠른 검색을 위해 사용됩니다.
- 파일 시스템: 디렉터리 탐색에 활용됩니다.
- 이벤트 관리 시스템: 시간 순서로 정렬된 이벤트 관리에 사용됩니다.
💡 도움이 되셨다면 댓글과 공감 부탁드립니다! 😊
📌 더 많은 알고리즘 풀이와 프로그래밍 자료는 블로그에서 확인하세요!
✉️ 문의나 피드백은 댓글이나 이메일로 남겨주세요.
'Computer Science > 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조 & 알고리즘] 힙(Heap)으로 우선순위 큐 구현하기 (feat. Lazy Deletion) (0) | 2025.02.25 |
|---|---|
| [자료구조 & 알고리즘] 이진 검색 트리 (feat. 트리) (0) | 2025.02.11 |
| [자료구조 & 알고리즘] 해시 테이블(Hash Table) (0) | 2025.02.05 |
| [자료구조 & 알고리즘] 이분 탐색 (Binary Search) (0) | 2025.02.03 |
| [자료구조 & 알고리즘] 그리디 알고리즘(Greedy Algorithm) (0) | 2025.02.02 |



