728x90
반응형
2025.02.02 - [Computer Science/자료구조 & 알고리즘] - [자료구조 & 알고리즘] 그리디 알고리즘(Greedy Algorithm)
[자료구조 & 알고리즘] 그리디 알고리즘(Greedy Algorithm)
그리디 알고리즘(Greedy Algorithm)1. 개요그리디 알고리즘(Greedy Algorithm)이란 현재 단계에서 가장 최적의 선택을 반복하여 문제를 해결하는 알고리즘입니다. 탐욕법이라고도 불리는 이 방식은 매 순
rnasterofmysea.tistory.com
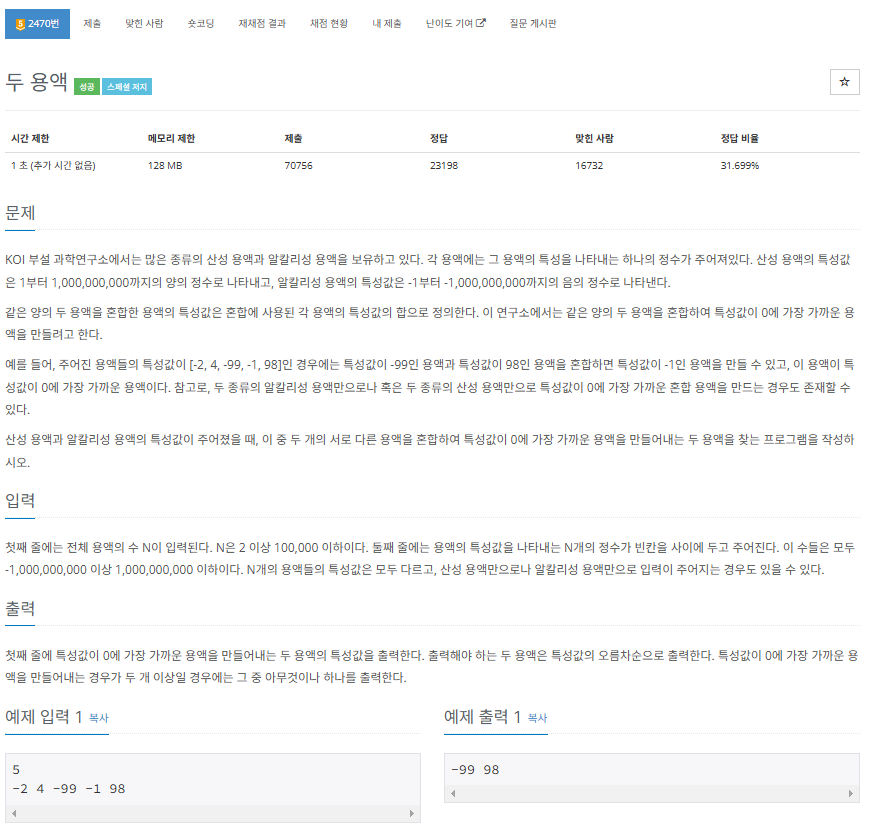
백준 2470번: 두 용액 (https://www.acmicpc.net/problem/2470)
1. 문제 설명
백준 2470번 문제는 두 개의 용액을 선택하여 그 합이 0에 가장 가까운 값을 찾는 문제입니다. 주어진 용액 리스트에서 두 개를 선택하여 합이 0에 가장 가까운 두 용액을 찾아야 합니다.
입력
- 첫 번째 줄: 용액의 개수 NN (2 ≤ NN ≤ 100,000)
- 두 번째 줄: NN개의 정수 (각 용액의 특성값, -10억 이상 10억 이하)
출력
- 합이 0에 가장 가까운 두 용액의 특성값을 오름차순으로 출력
예제 입력
5
-2 4 -99 -1 98
예제 출력
-2 4
2. 문제 해결 접근
이 문제는 투 포인터(Two Pointer) 알고리즘을 사용하여 해결할 수 있습니다.
전체적인 접근 방식은 다음과 같습니다:
- 리스트를 정렬합니다.
- 양 끝에서 시작하는 두 개의 포인터(point1, point2)를 사용하여 탐색을 진행합니다.
- 현재 두 포인터가 가리키는 용액의 합을 계산하고, 합이 0에 가까운지 갱신합니다.
- 만약 합이 0보다 작다면 왼쪽 포인터를 오른쪽으로 이동하고, 0보다 크다면 오른쪽 포인터를 왼쪽으로 이동합니다.
- 위 과정을 포인터가 교차할 때까지 반복하여 최적의 두 용액을 찾습니다.
3. 코드 구현
"""
python_boj_2470_두 용액
https://www.acmicpc.net/problem/2470
"""
import sys
input = sys.stdin.readline
N = int(input().strip()) # 정수 N 입력
arry = list(map(int, input().strip().split())) # 리스트로 변환
arry.sort() # 정렬
len_arry = len(arry)
count_al = sum(1 for x in arry if x < 0) # 음수 개수
count_san = len_arry - count_al # 양수 개수
# 모든 숫자가 음수인 경우 → 절댓값이 작은 두 개 출력
if count_al == len_arry:
print(arry[-2], arry[-1])
# 모든 숫자가 양수인 경우 → 가장 작은 두 개 출력
elif count_san == len_arry:
print(arry[0], arry[1])
else:
# 투 포인터 활용하여 0에 가까운 값 찾기
result = float('inf')
result_point1 = 0
result_point2 = 0
point1 = 0
point2 = len_arry - 1 # 마지막 원소부터 시작
while point1 < point2:
temp_result = abs(arry[point1] + arry[point2])
if temp_result < result:
result_point1 = point1
result_point2 = point2
result = temp_result
if arry[point1] + arry[point2] < 0:
point1 += 1
else:
point2 -= 1
print(arry[result_point1], arry[result_point2])1. 입력 처리 및 정렬
import sys
input = sys.stdin.readline
N = int(input().strip()) # 정수 N 입력
arry = list(map(int, input().strip().split())) # 리스트로 변환
arry.sort() # 정렬
- sys.stdin.readline()을 사용하여 입력을 빠르게 처리합니다.
- N은 용액의 개수를 의미합니다.
- map(int, input().strip().split())을 사용하여 입력값을 정수 리스트로 변환합니다.
- 리스트를 정렬하여 음수 → 양수 순서로 정리합니다.
정렬하면 투 포인터 알고리즘을 활용하기 쉬워집니다.
2. 음수와 양수 개수 파악
len_arry = len(arry)
count_al = sum(1 for x in arry if x < 0) # 음수 개수
count_san = len_arry - count_al # 양수 개수
- count_al: 리스트에서 음수의 개수를 계산합니다.
- count_san: 전체 개수에서 count_al을 빼서 양수 개수를 계산합니다.
- 이 정보를 활용하여 특별한 경우(모든 숫자가 양수 또는 음수일 때)를 처리합니다.
3. 모든 숫자가 음수 또는 양수인 경우 예외 처리
# 모든 숫자가 음수인 경우 → 절댓값이 작은 두 개 출력
if count_al == len_arry:
print(arry[-2], arry[-1])
# 모든 숫자가 양수인 경우 → 가장 작은 두 개 출력
elif count_san == len_arry:
print(arry[0], arry[1])
(1) 모든 숫자가 음수인 경우
- count_al == len_arry라면 모든 값이 음수입니다.
- 음수의 절댓값이 작은 두 개를 선택하기 위해 가장 큰 두 개의 숫자(arry[-2], arry[-1])를 출력합니다.
(2) 모든 숫자가 양수인 경우
- count_san == len_arry라면 모든 값이 양수입니다.
- 0에 가장 가까운 두 개의 숫자는 가장 작은 두 개의 양수(arry[0], arry[1])입니다.
이 예외 처리를 먼저 수행하면, 이후 양수와 음수가 섞여 있는 경우만 고려하면 됩니다.
4. 투 포인터 알고리즘을 활용하여 최적의 두 용액 찾기
else:
# 투 포인터 활용하여 0에 가까운 값 찾기
result = float('inf') # 최소값 초기화 (무한대)
result_point1 = 0 # 결과로 출력할 첫 번째 용액의 인덱스
result_point2 = 0 # 결과로 출력할 두 번째 용액의 인덱스
point1 = 0 # 왼쪽 포인터 (음수부터 시작)
point2 = len_arry - 1 # 오른쪽 포인터 (양수부터 시작)
while point1 < point2:
temp_result = abs(arry[point1] + arry[point2]) # 두 용액의 합의 절댓값 계산
# 0에 더 가까운 값 발견 시 갱신
if temp_result < result:
result_point1 = point1
result_point2 = point2
result = temp_result
# 합이 0보다 작으면 더 큰 값이 필요하므로 point1 이동
if arry[point1] + arry[point2] < 0:
point1 += 1
# 합이 0보다 크면 더 작은 값이 필요하므로 point2 이동
else:
point2 -= 1
print(arry[result_point1], arry[result_point2])
초기화
- result: 현재까지 찾은 0에 가장 가까운 합의 절댓값을 저장 (float('inf')로 초기화)
- result_point1, result_point2: 최적의 두 용액의 인덱스 저장
- point1: 왼쪽 포인터 (음수부터 탐색 시작)
- point2: 오른쪽 포인터 (양수부터 탐색 시작)
반복문 (while point1 < point2)
- point1 < point2가 만족하는 동안 두 용액을 선택하여 합을 계산합니다.
합이 0에 더 가까운지 확인
- 현재 선택된 두 용액의 합을 temp_result로 저장합니다.
- 기존 result보다 작은 경우, 더 0에 가까운 조합이므로 갱신합니다.
temp_result = abs(arry[point1] + arry[point2]) # 두 용액의 합의 절댓값 계산
if temp_result < result:
result_point1 = point1
result_point2 = point2
result = temp_result
포인터 이동 전략
- arry[point1] + arry[point2] < 0: 합이 0보다 작으면, 더 큰 값을 찾아야 하므로 왼쪽 포인터 이동
- arry[point1] + arry[point2] > 0: 합이 0보다 크면, 더 작은 값을 찾아야 하므로 오른쪽 포인터 이동
if arry[point1] + arry[point2] < 0:
point1 += 1
else:
point2 -= 14. 예제 테스트
입력 예제
5
-2 4 -99 -1 98
과정
| left | right | arr[left] | arr[right] | 합 최적값 | 갱신 여부 |
| 0 | 4 | -99 | 98 | -1 | ✅ 갱신 |
| 1 | 4 | -2 | 98 | 96 | ❌ |
| 1 | 3 | -2 | 4 | 2 | ❌ |
| 1 | 2 | -2 | -1 | -3 | ❌ |
출력
-2 4
💡 도움이 되셨다면 댓글과 공감 부탁드립니다! 😊
📌 더 많은 알고리즘 풀이와 프로그래밍 자료는 블로그에서 확인하세요!
✉️ 문의나 피드백은 댓글이나 이메일로 남겨주세요.
728x90
반응형
'Computer Science > 알고리즘 문제' 카테고리의 다른 글
| Python - [백준 21939] 문제 추천 시스템 Version 1 (0) | 2025.02.27 |
|---|---|
| Python - [백준 7662] 이중 우선순위 큐 (feat. 힙, 우선순위큐, Lazy Deletion) (0) | 2025.02.26 |
| Python - [백준 12789] 도키도키 간식드리미 (feat. 스택) (0) | 2025.02.09 |
| C - [Backjoon 18869] 멀티버스 II (feat. 이분탐색, 좌표압축) (0) | 2025.02.08 |
| C - [백준 18870] 좌표 압축 (feat. 이분탐색, 퀵정렬) (0) | 2025.02.07 |



