PART02: 빅데이터 탐색
CHAPTER02 데이터 전처리

참고 자료:
https://ko.wikipedia.org/wiki/%EC%A3%BC%EC%84%B1%EB%B6%84_%EB%B6%84%EC%84%9D
주성분 분석 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 중심점의 좌표가(1,3)이고, (0.878, 0.478)방향으로 3, 이와 수직한 방향으로 1의 표준편차를 가지는 다변량 정규분포에 대한 주성분 분석. 화살표의 길이는 공분산
ko.wikipedia.org
[P02CH01S02] 분석 변수 처리
1. 변수 선택
1.1. 변수 모형의 분류
- 전체모형(FML Full Model): 모든 독립변수를 사용한 모형으로 정의한다.
- 축소모형(RM, Reduced Model): 전체 모형에서 사용된 변수의 개수를 줄여서 얻은 모형
- 영 모형(NM: Null Mode): 독립변수가 하나도 없는 모형을 의미한다.
1.2. 변수의 선택 방법
1) 전진 선택방법(Forward Selection)
유의! 한번 추가된 변수는 제거하지 않는 것이 원칙 (전진 & 후진 공통)
1. 시작: 영 모형(Null Model)에서 시작
2. 변수 선택
- 단순상관계수 계산: 모든 독립 변수와 종속 변수 간의 단순 상관계수를 계산합니다.
- 가장 큰 절대값 선택: 단순 상관계수의 절대값이 가장 큰 독립 변수를 선택합니다. 이 변수가 종속 변수와 가장 강한 선형 관계를 가진다고 가정합니다.
3. 유의성 검증
- 부분 F검정(F-test) 수행: 선택된 변수를 모형에 추가한 후, 이 변수가 모형에 유의미한지 검증하기 위해 부분 F검정을 시행합니다.
- F 통계량: 이 통계량은 모형의 설명력을 평가하는 지표로, 값이 클수록 해당 변수가 모형에 유의미한 영향을 미친다고 볼 수 있습니다.
- 유의성 판단: F검정 결과가 유의미하다면(일반적으로 p-value가 0.05 미만), 해당 변수를 모형에 포함시킵니다. 유의미하지 않다면 변수 선택 과정을 중단합니다.
4. 반복
- 과정 반복: 새로운 변수가 추가된 모형을 기준으로 다시 남은 독립 변수들에 대해 단순상관계수를 계산하고, 가장 유의미한 변수를 선택하여 모형에 추가하는 과정을 반복합니다.
- 중단 조건: 더 이상 유의미한 변수가 없을 때까지 이 과정을 반복합니다.
단순상관계수(Simple Correlation Coefficient)는 두 변수 간의 선형 관계를 측정하는 지표입니다. 이 계수는 피어슨 상관계수(Pearson Correlation Coefficient)라고도 불리며, 일반적으로 rr로 표기됩니다. 단순상관계수는 두 변수가 얼마나 강하게, 그리고 어떤 방향으로 관련되어 있는지를 나타냅니다.
단순상관계수의 특징
범위: 단순상관계수는 −1−1부터 +1+1 사이의 값을 가집니다.
r=1: 완벽한 양의 선형 관계 (한 변수가 증가하면 다른 변수도 증가)
r=−1: 완벽한 음의 선형 관계 (한 변수가 증가하면 다른 변수는 감소)
r=0: 선형 관계가 없음 (두 변수는 서로 독립적)
2) 후진 선택 방법
유의! 한번 추가된 변수는 제거하지 않는 것이 원칙 (전진 & 후진 공통)
- 시작: 모든 독립 변수를 포함한 전체 모형(FM) 에서 시작합니다.
- 변수 제거:
- 각 변수의 p-value를 확인합니다.
- 가장 p-value가 큰 변수(가장 유의미하지 않은 변수)를 제거합니다.
- 만약 p-value가 기준(예: 0.05)보다 크면 제거, 작으면 유지합니다.
- 반복: 변수를 제거한 후, 다시 남은 변수들의 p-value를 확인하며 과정을 반복합니다.
- 종료: 모든 변수의 p-value가 기준보다 작아지면 종료합니다.
3) 단계적 선택법(Stepwise Selection)
- 전진 선택법과 후진 선택법의 보완방법
- 전진 선택법을 통해 가장 유의한 변수를 모형에 포함 후 나머지 변수들에 대해 후진 선택법을 적용하여 새롭게 유의하지 않는 변수들을 제거합니다.
- 제거된 변수는 다시 모형에 포함하지 않으며 유의한 설명변수가 존재하지 않을때 까지 반복합니다.
다음은 보완된 "차원 축소" 정리입니다. 내용의 논리적 흐름을 개선하고, 개념 설명을 보다 명확하게 정리하였습니다. 또한, 실무에서의 활용 사례와 추가적인 차원 축소 방법을 보강하였습니다.
2. 차원 축소 (Dimensionality Reduction)
2.1 .차원 축소란?
차원 축소(Dimensionality Reduction)란 데이터의 변수(특성)의 수를 줄이는 과정입니다. 이는 데이터 분석의 효율성을 높이고, 머신러닝 모델의 성능을 향상시키기 위해 사용됩니다.
차원 축소는 다음과 같은 목적을 가집니다.
- 데이터의 계산 비용 절감: 변수가 많을수록 연산량이 증가하여 학습 속도가 느려짐.
- 모델의 일반화 성능 향상: 불필요한 변수를 제거하여 과적합(Overfitting) 방지.
- 데이터의 해석력 증대: 중요한 특징을 남겨 모델의 가독성을 높임.
- 차원의 저주(Curse of Dimensionality) 해결: 고차원 데이터에서 발생하는 문제를 완화.
2.2. 차원의 저주(Curse of Dimensionality)
고차원 데이터에서는 데이터가 희소(Sparse)해지며, 거리 기반 알고리즘의 성능이 저하됩니다. 또한, 모델이 학습 데이터에 과적합할 가능성이 커집니다.
✔ 해결 방법:
- 차원을 줄인다 → 불필요한 변수를 제거하고 핵심 변수만 남김.
- 데이터 수를 늘린다 → 더 많은 샘플을 확보하여 고차원에서의 희소성을 완화.
2.3. 차원 축소의 유형
차원 축소 방법은 크게 특징 선택(Feature Selection)과 특징 추출(Feature Extraction) 두 가지로 구분됩니다.
- 특징 선택 (Feature Selection)
- 기존 변수 중 중요한 변수를 선택하여 차원을 줄이는 방법.
- 예: 상관계수 분석, 결정 트리 기반 중요도 분석, Lasso 회귀.
- 특징 추출 (Feature Extraction)
- 기존 변수들을 조합하여 새로운 변수를 생성하는 방법.
- 예: 주성분 분석(PCA), 특이값 분해(SVD), t-SNE, UMAP.
2.4 주요 차원 축소 방법
1) 주성분 분석(PCA, Principal Component Analysis)
- 개념: 데이터의 분산을 최대한 보존하는 방향으로 새로운 축(주성분)을 정의하여 차원을 축소하는 방법.
- 특징:
- 첫 번째 주성분(PC1)이 가장 많은 분산을 설명하며, 두 번째 주성분(PC2)은 첫 번째 주성분과 직교함.
- 비지도 학습(Unsupervised Learning) 기법.
- 입력 데이터의 선형 결합을 이용하여 차원 축소 수행.
- 활용 사례:
- 이미지 압축 (얼굴 인식)
- 노이즈 제거
- 데이터 시각화 (고차원 데이터를 2D 또는 3D로 변환)
✔ PCA 한계점: 선형적인 특성만 고려하므로, 비선형 데이터에서는 성능이 저하될 수 있음.
아래 블로그에 dong1 님께서 잘 정리해 두셨습니다.
PCA에 대한 자세한 내용은 하단 블로그 참고하면 도움이 될 것 같습니다.
https://ddongwon.tistory.com/114
PCA (Principal Component Analysis) : 주성분 분석 이란?
1. PCA (주성분 분석) PCA는 대표적인 dimensionality reduction (차원 축소)에 쓰이는 기법으로, 머신러닝, 데이터마이닝, 통계 분석, 노이즈 제거 등 다양한 분야에서 널리 쓰이는 녀석이다. 쉽게 말해 PC
ddongwon.tistory.com
2) 공통 요인 분석(Common Factor Analysis, FA)
- 개념: 여러 변수에서 공통된 요인을 찾아 변수 개수를 줄이는 방법.
- 특징:
- PCA와 달리 데이터 내 공통된 ‘잠재 변수’를 추출하는 방식.
- 주로 심리학, 사회과학 등 설문 조사 분석에서 활용.
- 활용 사례:
- 설문조사에서 주요 응답 패턴 도출.
- 투자 포트폴리오에서 상관관계가 높은 변수 그룹화.
✔ FA vs PCA:
- PCA는 데이터의 전체적인 분산을 보존하는 방향,
- FA는 공통된 요인을 찾고 데이터 간 상관관계를 분석하는 방법.
3) 특이값 분해(SVD, Singular Value Decomposition)
- 개념: 행렬을 세 개의 행렬로 분해하여 중요한 정보만 남기는 방식으로 차원 축소를 수행.
- 특징:
- PCA와 유사하나, 대규모 희소 행렬(Sparse Matrix)에도 적용 가능.
- 행렬을 분해하여 노이즈를 제거하는 데 유용.
- 활용 사례:
- 추천 시스템 (Netflix 추천 알고리즘)
- 텍스트 마이닝 (잠재 의미 분석, LSA)
- 이미지 압축 (픽셀 데이터 차원 축소)
4) t-SNE (t-Distributed Stochastic Neighbor Embedding)
- 개념: 데이터 포인트 간의 유사도를 고려하여 2D 또는 3D로 시각화하는 비선형 차원 축소 기법.
- 특징:
- 고차원 데이터의 복잡한 구조를 유지하면서 시각화 가능.
- 데이터의 전반적인 구조보다는 개별 클러스터 간 관계를 강조.
- 활용 사례:
- 이미지 데이터 군집 분석 (손글씨 숫자 분류)
- 유전자 데이터 분석
✔ 단점: 차원 축소 결과가 반복할 때마다 다를 수 있으며, 해석이 어려울 수 있음.
5) UMAP (Uniform Manifold Approximation and Projection)
- 개념: 데이터의 구조를 보존하면서 낮은 차원으로 변환하는 비선형 차원 축소 기법.
- 특징:
- t-SNE보다 빠르고, 데이터의 전반적인 구조를 더 잘 보존.
- 머신러닝 및 데이터 시각화에서 강력한 성능 발휘.
- 활용 사례:
- 클러스터링 및 데이터 시각화.
- 딥러닝의 특징 벡터 분석.
2.5 차원 축소 방법 비교
| PCA | 데이터의 분산을 최대화하는 주성분 추출. 선형 방법. | 데이터 시각화, 노이즈 제거, 특징 추출 |
| 공통 요인 분석 | 변수 간 공통된 요인 추출. 잠재 변수 모델링. | 설문조사 분석, 사회과학 연구 |
| SVD | 행렬 분해를 통한 정보 보존. 희소 행렬에 유용. | 추천 시스템, LSA(텍스트 마이닝) |
| t-SNE | 비선형 구조를 유지한 2D/3D 변환 | 이미지 분류, 유전자 데이터 분석 |
| UMAP | t-SNE보다 빠르고 전반적인 구조 유지 | 고차원 데이터 클러스터링 |
3. 파생 변수의 생성
3.1 파생 변수(Derived Variable)란?
파생 변수(Derived Variable)란 기존 데이터에서 특정 연산, 변환, 혹은 규칙을 적용하여 새로운 의미를 가진 변수를 생성하는 것을 의미합니다.
이는 분석 목적에 맞게 데이터를 가공하여 모델의 예측 성능을 높이고, 데이터의 해석력을 향상시키는 역할을 합니다.
📌 파생 변수의 특징
- 기존 데이터를 기반으로 생성됨.
- 특정 조건(if-else)이나 함수(산술 연산, 그룹화, 변환 등)을 적용하여 의미를 부여.
- 데이터 분석가의 주관적 판단이 개입될 수 있어 논리적 타당성이 중요.
3.2 요약 변수(Summary Variable)란?
요약 변수(Summary Variable)는 원래 데이터의 개별 값을 종합하여 집계(Aggregation)한 변수입니다.
📌 요약 변수의 특징
- 기존 데이터의 개별 값을 집계하여 하나의 대표값으로 요약.
- 평균(mean), 합(sum), 최소(min), 최대(max), 표준편차(std) 등의 통계를 사용.
- 데이터의 전반적인 경향을 분석할 때 활용됨.
4. 변수 변환 (Variable Transformation)
4.1 변수 변환이란?
변수 변환(Variable Transformation)이란 기존 데이터의 값을 일정한 규칙에 따라 변형하여 모델의 성능을 개선하고 데이터의 분포를 조정하는 과정입니다.
📌 변수 변환의 목적
- 정규성(Normality) 확보
- 많은 통계 모델과 머신러닝 알고리즘은 정규 분포(정상 분포)를 가정하므로, 데이터의 분포를 정규 분포에 가깝게 변환해야 함.
- 스케일(Scale) 조정
- 변수들의 크기 차이가 클 경우, 학습 속도 저하 및 특정 변수가 모델에 과도한 영향을 줄 수 있음 → 정규화(Scaling) 필요.
- 이상치(Outlier) 완화
- 이상치가 극단적으로 클 경우, 회귀 모델 등의 성능 저하 발생 → 로그 변환, Box-Cox 변환 등을 활용해 완화.
- 해석력 향상
- 변수 간 관계를 더욱 선형적으로 만들거나, 새로운 해석이 가능하도록 변환.
4.2 변수 변환의 방법
1. 범주형 변환 (Categorical Transformation)
📌 범주형 변수(Categorical Variable)는 모델이 이해할 수 있도록 수치형으로 변환해야 함.
변환 방법:
- One-Hot Encoding: 범주의 개수가 적을 때 사용. (예: 성별 → {남자: [1,0], 여자: [0,1]})
- Label Encoding: 범주의 개수가 많을 때 사용. (예: {서울=0, 부산=1, 대구=2})
- Target Encoding: 카테고리를 해당 값의 평균이나 통계값으로 변환.
4.2. 정규화 (Normalization)
데이터의 크기 차이를 줄이고, 비교 가능하도록 변환하는 기법.
(1) 최소-최대 정규화 (Min-Max Normalization)
- 데이터 값을 0과 1 사이의 범위로 변환.
- 활용: 거리 기반 모델(kNN, K-Means 등)

(2) Z-score 정규화 (Standardization)
- 평균 0, 표준편차 1을 갖도록 변환.
- 활용: 선형 회귀, 로지스틱 회귀, SVM 등

4.3. 로그 변환 (Log Transformation)
- 데이터의 분포가 오른쪽으로 긴 분포(Positive Skewed Distribution)를 보일 때, 데이터 범위를 줄이고 정규성을 향상시키는 변환 기법. 큰 값을 상대적으로 작게 줄이고, 작은 값은 상대적으로 크게 만
- 활용: 소득 데이터, 가격 데이터 등.

📌 주의사항: 로그 함수는 0 이하의 값에서 정의되지 않으므로, log(X + 1) 또는 log(X + c) 형태로 변환하는 경우가 많음.
4.4. 역수 변환 (Reciprocal Transformation)
- 데이터 값이 클수록 변환 후 값이 작아지는 형태.
- 활용: 데이터의 비율(scale)을 조정할 때 사용.
- 주의사항: 0이 포함된 데이터에서는 사용할 수 없음.
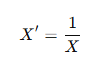
4.5. 지수 변환 (Exponential Transformation)
- 데이터의 분포가 왼쪽으로 긴 분포( Negative Skewed Distribution)를 보일 때, 데이터 범위를 줄이고 정규성을 향상시키는 변환 기법. 은 값을 상대적으로 크게 늘리고, 큰 값은 상대적으로 더 크게 만듬
- 활용: 데이터 값이 작은 범위에서 차이가 클 때.

4.6. 제곱근 변환 (Square Root Transformation)
- 데이터 분포가 비대칭적일 때, 정규성 확보를 위해 사용.
- 활용: 포아송 분포(Poisson Distribution)에서 변동성을 줄일 때 유용.

포아송 분포(Poisson Distribution)는 특정 시간 또는 공간 내에서 발생하는 드물고 독립적인 사건의 횟수를 모델링하는 이산형 확률 분포입니다. 이 분포는 단위 시간 또는 단위 공간에서 사건이 발생할 확률을 나타내는 데 사용됩니다.
7. 분포 형태별 정규 분포로 변환
데이터의 분포가 정규 분포를 따르지 않을 경우, 통계적 기법을 이용하여 정규 분포로 변환.
📌 변환 방법
- 왼쪽으로 치우친 분포(Left Skewed) → 제곱 변환 (X²)
- 오른쪽으로 치우친 분포(Right Skewed) → 로그 변환(log X)
- 정규 분포에 가까운 분포 → Box-Cox 변환

4.8. Box-Cox 변환 (Box-Cox Transformation)
- 다양한 지수 변환을 포함하는 가장 일반적인 정규화 방법.
- 특정 지수(λ, 람다)를 찾아 데이터의 정규성을 최적화.
- 활용: 선형 회귀 모델, 정규성 검정을 위한 사전 처리.
- 장점: 데이터의 분포 형태에 맞게 최적의 변환을 자동으로 찾아줌.

5. 불균형 데이터 (Imbalanced Data)
5.1 불균형 데이터의 문제점
불균형 데이터(Imbalanced Data)란, 데이터셋에서 특정 클래스(범주)의 샘플 수가 다른 클래스보다 압도적으로 많거나 적은 경우를 의미합니다. 예를 들어, 부정거래 탐지(Fraud Detection), 의료 진단(Disease Detection), 고장 예측(Failure Prediction) 등의 문제에서 일반적인 클래스(정상 거래, 건강한 사람, 정상 기계)는 많지만, 특이한 클래스(부정 거래, 질병 환자, 고장 기계)는 매우 적은 경우가 많습니다.
📌 불균형 데이터가 문제가 되는 이유
- 모델의 예측 성능 왜곡
- 모델이 다수 클래스를 중심으로 학습하여, 소수 클래스에 대한 예측 성능이 저하됨.
- 예: 신용카드 부정 거래 탐지에서 99%의 데이터가 정상 거래라면, 단순한 모델이 모든 거래를 "정상"으로 예측해도 99% 정확도를 보일 수 있음.
- 잘못된 평가 지표
- 단순한 정확도(Accuracy)는 불균형 데이터에서 무의미할 수 있음.
- 예:
- 정상 거래(99%) + 부정 거래(1%) 데이터에서, 모델이 모두 정상으로 예측하면 정확도 99%지만, 실제로는 부정 거래를 탐지하지 못하는 문제가 발생.
- 모델 학습의 어려움
- 모델이 소수 클래스의 패턴을 학습하지 못하고 무시하는 경향이 있음.
- 데이터의 클래스 비율이 극단적으로 불균형하면 모델이 수렴하는 데 어려움을 겪음.
5.2 불균형 데이터의 처리 방법
1) 가중치 균형 방법 (Class Weight Balancing)
모델 학습 시, 다수 클래스보다 소수 클래스에 더 높은 가중치(weight)를 부여하여 균형을 맞추는 방법.
📌 가중치 설정 방식
- 고정 비율(Fixed Ratio)
- 사용자가 특정 비율을 직접 설정하여 가중치를 부여.
- 예: 클래스 A(1) : 클래스 B(10) → 클래스 B에 가중치 10배 부여
- 최적 비율(Optimal Ratio, Inverse Frequency Weighting)
- 각 클래스의 샘플 개수를 반영하여 자동으로 가중치를 조정하는 방식.
- 소수 클래스의 가중치를 높여 모델이 이를 더 중요하게 학습하도록 유도.
✔ 활용 예시
- Scikit-learn의 class_weight='balanced' 옵션 사용.
- 로지스틱 회귀(Logistic Regression), 랜덤 포레스트(Random Forest), XGBoost 등에서 활용 가능.
2) 샘플링 기법 (Sampling Methods)
데이터 샘플의 개수를 조정하여 클래스 균형을 맞추는 방법.
(1) 언더샘플링 (Under-Sampling)
- 다수 클래스의 샘플 수를 줄여 소수 클래스와 균형을 맞추는 방법.
- 장점: 데이터의 균형이 맞춰져 계산 비용이 줄어듦.
- 단점: 중요한 정보를 가진 데이터를 제거할 위험이 있음.
✔ 대표적인 언더샘플링 기법
- 랜덤 언더샘플링(Random Under-Sampling, RUS)
- 다수 클래스에서 데이터를 무작위로 제거.
- NearMiss
- 다수 클래스의 데이터 중, 소수 클래스와 거리가 가까운 데이터를 우선적으로 제거.
✅ 활용 예시
- 대량의 정상 데이터(90%)와 적은 비율의 부정 거래 데이터(10%)가 있을 때, 정상 데이터를 랜덤하게 줄여 균형을 맞춤.
(2) 오버샘플링 (Over-Sampling)
- 소수 클래스의 샘플 수를 증가시켜 다수 클래스와 균형을 맞추는 방법.
- 장점: 원래 데이터를 유지하면서도 균형을 맞출 수 있음.
- 단점: 단순 복제 시 과적합(Overfitting) 위험이 존재.
✔ 대표적인 오버샘플링 기법
- 랜덤 오버샘플링(Random Over-Sampling, ROS)
- 소수 클래스 데이터를 단순 복제하여 개수를 증가.
- SMOTE (Synthetic Minority Over-sampling Technique)
- 소수 클래스의 데이터를 랜덤하게 선택하여 새로운 합성 데이터(Synthetic Data)를 생성.
- 기존 데이터 포인트 간의 거리를 기반으로 새로운 샘플을 만들어 과적합을 방지.
✅ 활용 예시
- 의료 데이터에서 질병 환자가 적을 경우, SMOTE 기법을 사용해 가상의 환자 데이터를 생성하여 학습 성능을 개선.
5.3 불균형 데이터 처리 방법 비교
| 가중치 균형 (Class Weighting) | 모델 학습 시, 소수 클래스에 높은 가중치 부여 | 데이터 삭제 없이 균형 유지 | 일부 모델에서만 지원 | 로지스틱 회귀, 랜덤 포레스트 |
| 언더샘플링 (Under-Sampling) | 다수 클래스 데이터 제거 | 계산 비용 감소 | 데이터 손실 가능 | 대량의 정상 데이터가 있는 경우 |
| 오버샘플링 (Over-Sampling) | 소수 클래스 데이터를 증가 | 데이터 보존 가능 | 과적합 위험 | 의료 데이터, 사기 탐지 |
| SMOTE | 소수 클래스를 합성하여 샘플 증가 | 과적합 방지 | 노이즈 데이터가 포함될 수 있음 | 금융, 의료 데이터 |
6. 인코딩 (Encoding)
6.1 인코딩이란?
인코딩(Encoding)이란, 범주형 데이터(Categorical Data)를 컴퓨터가 처리할 수 있도록 수치형 데이터(Numerical Data)로 변환하는 과정입니다.
머신러닝 모델은 숫자 데이터만 입력받을 수 있으므로, 텍스트나 범주형 변수를 수치형 변수로 변환하는 것이 필수적입니다.
📌 범주형 데이터 인코딩의 주요 방법:
- 레이블 인코딩(Label Encoding)
- 원-핫 인코딩(One-Hot Encoding)
- 타깃 인코딩(Target Encoding)
6.2 주요 인코딩 기법
1. 레이블 인코딩 (Label Encoding)
📌 개념:
- 각 범주(Category)에 고유한 정수(Label)를 할당하여 변환하는 방식.
- 단순하고 빠르지만, 값의 크기(순서) 정보가 포함되어 문제 발생 가능.
📌 예제:
| 서울 | 0 |
| 부산 | 1 |
| 대구 | 2 |
| 광주 | 3 |
📌 장점:
- 간단하고 메모리 사용이 적음.
- 트리 기반 모델(랜덤 포레스트, XGBoost)에서 사용 가능.
📌 단점:
- 순서가 없는 범주형 데이터에서 잘못된 의미를 부여할 위험.
- 예를 들어, "서울(0), 부산(1), 대구(2)"가 있으면 모델이 서울 < 부산 < 대구라는 잘못된 의미로 해석할 수 있음.
📌 활용 예시:
- 트리 기반 모델(랜덤 포레스트, XGBoost)에서 문제없이 사용 가능.
- 순서가 의미 있는 데이터(예: 학력 수준 "초등학교 < 중학교 < 고등학교")에 적합.
2. 원-핫 인코딩 (One-Hot Encoding)
📌 개념:
- 각 범주를 별도의 이진 벡터(Binary Vector)로 변환하는 방식.
- 고유한 범주 수만큼 열(column)을 생성하며, 해당 범주에 해당하는 위치에만 1, 나머지는 0을 할당.
📌 예제:
원본 데이터 서울 부산 대구 광주
| 서울 | 1 | 0 | 0 | 0 |
| 부산 | 0 | 1 | 0 | 0 |
| 대구 | 0 | 0 | 1 | 0 |
| 광주 | 0 | 0 | 0 | 1 |
📌 장점:
- 순서 정보가 포함되지 않으므로, 잘못된 관계가 학습되지 않음.
- 대부분의 머신러닝 알고리즘에서 안정적으로 사용 가능.
📌 단점:
- 고유한 범주의 개수가 많으면, 차원이 급격히 증가 (차원의 저주 발생).
- 예: 국가(195개) → 195개의 열(column)이 생성됨.
- 선형 모델(Linear Regression)에서는 다중공선성(Multicollinearity) 문제가 발생할 수 있음.
📌 활용 예시:
- 딥러닝(Neural Networks), 선형 모델(Logistic Regression) 등에서 자주 사용.
- 범주형 데이터가 많지 않은 경우(10개 이하의 범주) 효과적.
✔ 차원 축소 해결 방법:
- 범주 수가 많을 경우 차원 축소 기법(PCA, Feature Selection 등)을 적용.
- 대표적인 해결법으로 "차원 축소형 원-핫 인코딩 (Dummy Encoding)" 사용:
- n개의 범주 → n-1개의 컬럼만 사용.
3. 타깃 인코딩 (Target Encoding, Mean Encoding)
📌 개념:
- 각 범주(Category)를 해당 범주의 타깃(Target) 평균 값으로 변환하는 방식.
- 회귀 분석이나 분류 문제에서 사용 가능.
📌 예제 (분류 문제 예시):
| 서울 | 1, 1, 0, 1 | 0.75 |
| 부산 | 0, 0, 0, 1 | 0.25 |
| 대구 | 1, 0, 1, 0 | 0.50 |
| 광주 | 0, 0, 1, 1 | 0.50 |
📌 장점:
- 차원을 증가시키지 않아 효율적.
- 원-핫 인코딩처럼 메모리 낭비가 적음.
📌 단점:
- 학습 데이터의 타깃 값을 활용하므로 데이터 누수(Data Leakage) 위험 존재.
- K-Fold Cross Validation을 사용하여 과적합을 방지해야 함.
📌 활용 예시:
- 랜덤 포레스트, XGBoost, LightGBM 같은 트리 기반 모델에서 효과적.
- 고유한 범주가 많은 데이터에서 차원 증가를 피할 때 유용.
✔ 데이터 누수 방지 방법:
- K-Fold Cross Validation을 적용하여 각 Fold별 평균값을 계산.
- 랜덤한 노이즈(Smoothing) 값을 추가하여 과적합 방지.
6.3 인코딩 방법 비교
| 레이블 인코딩 | 각 범주를 정수(0, 1, 2...)로 변환 | 메모리 절약, 간단 | 순서 의미가 없는 데이터에 사용하면 문제 발생 | 트리 기반 모델 |
| 원-핫 인코딩 | 범주별 이진 벡터 생성 | 순서 정보 없음, 범주별 독립성 유지 | 고유 범주가 많으면 차원 증가 | 선형 모델, 신경망 |
| 타깃 인코딩 | 범주의 타깃 평균값으로 변환 | 차원 증가 없음, 효과적 | 데이터 누수 위험, 과적합 가능성 | 트리 기반 모델 (랜덤 포레스트, XGBoost) |
'자격증 > 빅데이터분석기사' 카테고리의 다른 글
| [P02CH02S02] 고급 데이터 탐색 (0) | 2025.03.15 |
|---|---|
| ✨ [P02CH02S01] 데이터 탐색 기초 (feat. 기초 통계량의 추출 및 이해) (0) | 2025.03.15 |
| [P02CH01S01] 데이터 정제 (1) | 2025.03.13 |
| PART 2: 빅데이터 탐색 (0) | 2025.03.13 |
| [P01CH02S02] 분석 작업 계획 (0) | 2025.03.12 |



