C - [백준 7576] 토마토 (feat. BFS, 연결요소, 최단거리)

참고 포스트

2024.12.25 - [Computer Science/자료구조 & 알고리즘] - C - [Backjoon 2178] 미로탐색 (feat. BFS & 최단거리 탐색)

C - [Backjoon 2178] 미로탐색 (feat. BFS & 최단거리 탐색)

참고 포스트https://rnasterofmysea.tistory.com/47 C - [Backjoon 1260] DFS와 BFS[참고 포스트]https://rnasterofmysea.tistory.com/45 [자료구조 & 알고리즘] 그래프 + DFS그래프에 대해 기초부터 차근차근 학습해보겠습니

rnasterofmysea.tistory.com

2024.12.22 - [Computer Science/자료구조 & 알고리즘] - [자료구조 & 알고리즘] 그래프 + BFS

[자료구조 & 알고리즘] 그래프 + BFS

이전 포스트 - 그래프 + DFShttps://rnasterofmysea.tistory.com/45 [자료구조 & 알고리즘] 그래프 + DFS그래프에 대해 기초부터 차근차근 학습해보겠습니다. 그래프는 DFS와 BFS를 이해하는 데 필수적인 자료구

rnasterofmysea.tistory.com

https://www.acmicpc.net/problem/7576

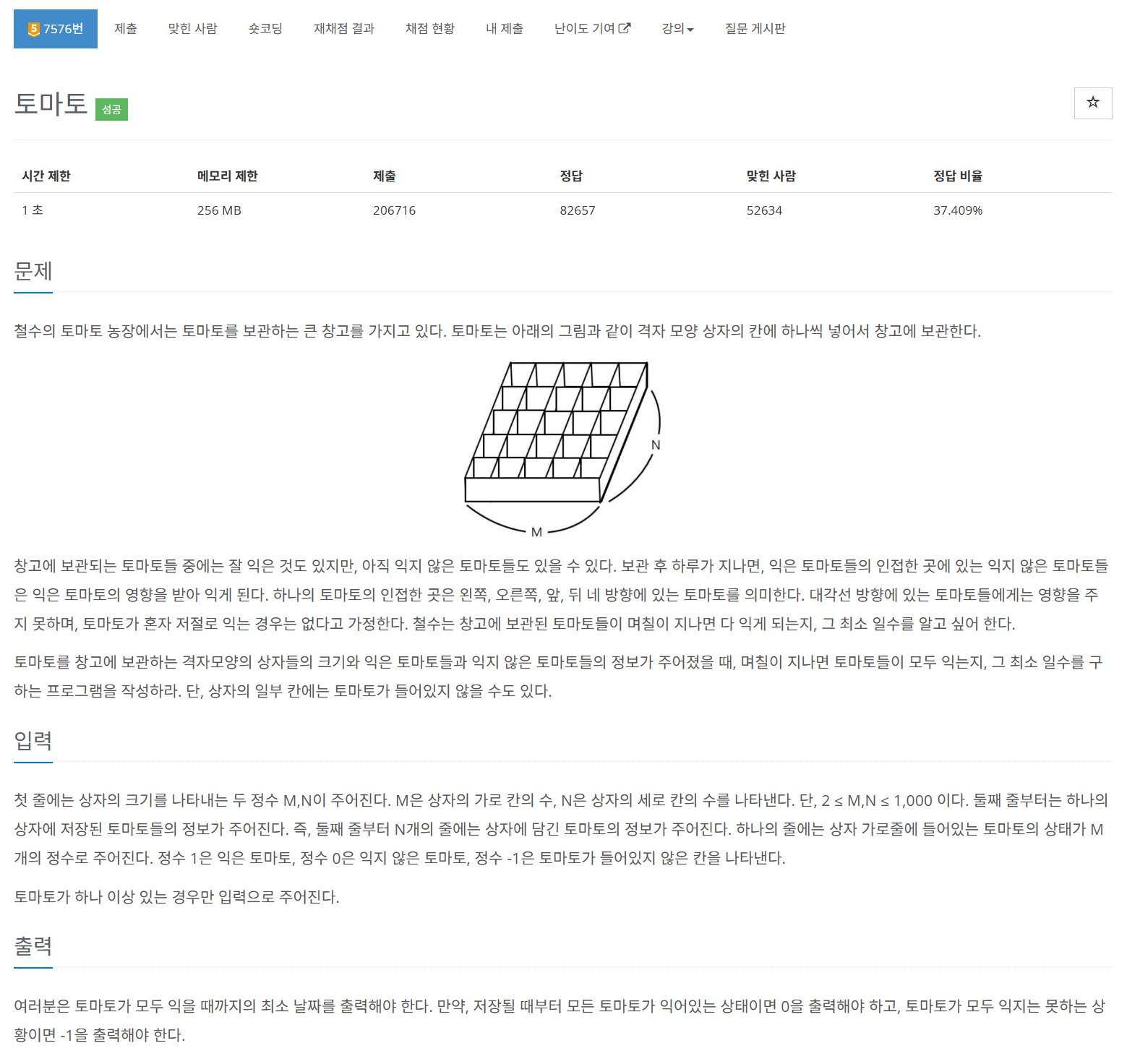
[BOJ 7576] 토마토

문제 설명

BOJ 7576 문제는 M×N 크기의 상자에서 익은 토마토(값 1)가 익지 않은 토마토(값 0)를 익히는 데 걸리는 최소 시간을 계산하는 문제입니다. 상자의 칸은 다음과 같은 값을 가집니다:

11: 익은 토마토
00: 익지 않은 토마토
−1-1: 비어 있는 칸

익은 토마토는 상하좌우로 하루에 1칸씩 익지 않은 토마토를 익힙니다. 모든 토마토가 익는 데 걸리는 최소 시간을 구하거나, 모두 익히는 것이 불가능하다면 -1을 출력해야 합니다.

문제 입력

첫 번째 줄: MM (가로 칸 수)과 NN (세로 칸 수), 2≤M,N≤1000
두 번째 줄부터: N×M 크기의 상자 상태.
- 11: 익은 토마토
- 00: 익지 않은 토마토
- −1-1: 비어 있는 칸

문제 출력

모든 토마토가 익는 데 걸리는 최소 시간을 출력.
모든 토마토가 익는 것이 불가능하다면 -1을 출력.

예제 입력 1

6 4
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 1

예제 출력 1

예제 입력 2

6 4
0 -1 0 0 0 0
-1 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 1

예제 출력 2

-1

예제 입력 3

6 4
1 -1 0 0 0 0
0 -1 0 0 0 0
0 0 0 0 -1 0
0 0 0 0 -1 1

예제 출력 3

예제 입력 4

5 5
-1 1 0 0 0
0 -1 -1 -1 0
0 -1 -1 -1 0
0 -1 -1 -1 0
0 0 0 0 0

예제 출력 4

예제 입력 5

2 2
1 -1
-1 1

예제 출력 5

Checkpoint

기존의 최단거리 문제인 미로 탐색(https://rnasterofmysea.tistory.com/51)와 그림(https://rnasterofmysea.tistory.com/52)이 합쳐져 있는 문제라고 생각합니다.

두 함수가 합쳐져 있는 이 문제는 BFS 함수의 내부 로직의 변화가 거의 없으나 BFS 시작과 노드를 enqueue 하는 부분의 약간의 변화가 있습니다.

상단의 미로 탐색 문제에서는 그래프(노드)를 입력 받은 후 0,0 인 지점부터 그래프의 크기(도착점) 만큼 상하좌우로 bfs를 진행하면서 거리를 갱신하면 되었습니다.

그림 문제에서는 연결요소를 찾은 후 해당 연결요소의 시작점부터 연결되어있는 노드의 갯수를 카운트하고 연결요소중 노드의 갯수가 가장 많은 그림을 찾아내면 되었습니다.

두 알고리즘을 합치면, 연결요소의 시작점을 찾고 그 지점부터 거리를 갱신하면 된다는 결론이 나는데, 해당 문제의 프로세스로 말을 바꿔보면, " 익은 토마토 (연결요소의 시작점, 1인 지점)을 찾고 그 지점 부터 연결되어 있는 노드를 탐색하며 탐색 시간을 기록하면 된다" 입니다.

여기까지 작성하고 제출했으나 실패하였습니다. 그 이유는 BFS 탐색 시작점에 있습니다.

이슈 사항 - BFS 시작 지점

1. 그림 문제에서의 BFS 시작 지점 처리

그림 문제의 특징:

그림 문제에서는 연결 요소를 탐색하는 방식으로 BFS를 수행합니다.
각 연결 요소의 시작점을 찾고, 해당 요소를 BFS로 탐색한 후, 다음 연결 요소를 찾아 동일한 과정을 반복합니다.
이 과정은 연결 요소들이 독립적이기 때문에 순차적으로 처리해도 아무 문제가 없습니다.

예시 코드:

// 전체 그래프 탐색
for (int i = 0; i < n; i++) {
    for (int j = 0; j < m; j++) {
        if (graph[i][j] == 1 && !visited[i][j]) {
            front = rear = 0; // 큐 초기화
            int area = bfs(j, i, n, m); // 해당 연결 요소의 크기를 반환
            if (area > max_area) {
                max_area = area;
            }
            count++;
        }
    }
}

동작 방식:

연결 요소의 시작점 찾기:
- 모든 좌표를 탐색하며, 아직 방문하지 않은 연결 요소의 시작점을 찾습니다.
BFS 탐색:
- 시작점부터 BFS를 수행해 연결 요소의 크기를 계산.
다음 연결 요소 탐색:
- 다른 연결 요소가 있다면, 새로운 시작점에서 동일한 작업을 반복.

2. 토마토 문제에서의 BFS 시작 지점

토마토 문제의 특징:

토마토는 순차적으로 익는 것이 아니라 동시에 익습니다.
그래프 안에 익은 토마토(값 1)가 여러 개일 경우, 이들을 개별적으로 처리하면 문제가 발생합니다.
- 익은 토마토가 여러 개라면, 동시에 상하좌우로 영향을 미쳐야 합니다.
따라서 모든 익은 토마토를 큐에 먼저 삽입하고 BFS를 시작해야 합니다.

문제가 발생하는 경우:

예를 들어, 다음과 같은 입력이 주어진 경우를 가정해봅시다:

입력:

순차적으로 BFS를 수행한 경우:

첫 번째 익은 토마토(왼쪽 상단)에서 BFS를 시작하면 오른쪽 상단의 토마토는 영향을 받지 않습니다.
이로 인해 오른쪽 상단의 익은 토마토는 다른 BFS로 처리되며, 최종적으로 올바른 시간이 계산되지 않을 수 있습니다.

동시에 BFS를 수행한 경우:

두 개의 익은 토마토(왼쪽 상단과 오른쪽 상단)가 동시에 BFS를 시작합니다.
이로 인해 두 토마토가 동시에 주변 토마토를 익히게 되어 올바른 결과를 보장합니다.

3. 해결 방법: BFS 시작 전 큐 초기화

토마토 문제에서는 모든 익은 토마토를 BFS 시작 전에 큐에 삽입해야 합니다.

구현 방식:

모든 익은 토마토를 큐에 삽입:
- 초기 상태에서 값이 1인 모든 좌표를 탐색하여 큐에 삽입합니다.
BFS 탐색 수행:
- 큐에서 하나씩 꺼내며 상하좌우로 영향을 미칩니다.

수정된 코드:

// 그래프 입력 및 큐 초기화
for (int i = 0; i < N; i++) {
    for (int j = 0; j < M; j++) {
        scanf("%d", &graph[i][j]);
        visited[i * M + j] = 0; // 방문 초기화
        if (graph[i][j] == 1) {
            enqueue(j, i); // 모든 익은 토마토를 큐에 삽입
        }
    }
}

// BFS 탐색
int max_time = bfs(M, N);

4. 정리: 그림 문제와 토마토 문제의 차이

특징 그림 문제 토마토 문제

연결성	각 연결 요소가 독립적.	여러 익은 토마토가 동시에 영향을 미침.
탐색 방식	시작점을 찾을 때마다 BFS를 실행.	모든 익은 토마토를 동시에 큐에 삽입하고 BFS 실행.
BFS 시작 시 큐 상태	큐에는 탐색할 단일 연결 요소의 시작점만 포함됨.	큐에는 익은 토마토(값 1)인 모든 좌표가 포함됨.
문제 발생 가능성	연결 요소가 독립적이므로 순차적으로 탐색해도 문제없음.	익은 토마토가 동시에 영향을 미치지 않으면 오류 발생.

문제 풀이

이 문제는 **BFS(너비 우선 탐색)**를 사용하여 해결합니다. BFS는 시작점에서 모든 방향으로 동일한 속도로 탐색을 확장하기 때문에, 최단 경로 문제에 적합합니다.

풀이 과정:

초기 상태 설정:
- 익은 토마토(값 1)의 모든 좌표를 큐에 삽입하고 탐색 시작.
- 익지 않은 토마토(값 0)는 BFS로 익혀야 하며, 비어 있는 칸(값 -1)은 제외.
BFS 탐색:
- 큐에서 노드를 하나씩 꺼내 상하좌우로 탐색.
- 탐색한 칸의 값(거리)을 이전 칸 +1로 갱신하여 최소 시간을 기록.
결과 계산:
- BFS 종료 후, 상자에 값 0이 남아 있다면 익히지 못한 토마토가 존재하는 것이므로 -1 출력.
- 그렇지 않다면, 갱신된 값 중 최대 값을 출력.

구현 코드

#include <stdio.h>
#include <stdlib.h>
/*
https://www.acmicpc.net/problem/7576
[BOJ 7576] 토마토

*/
// 전역 변수 선언
int graph[1000][1000];
int visited[1000000];
int queue[1000001][2];
int front = 0;
int rear = 0;
int dir[4][2] = {{0, 1}, {0, -1}, {-1, 0}, {1, 0}};

// 큐 삽입
void enqueue(int x, int y) {
    queue[rear][0] = x;
    queue[rear][1] = y;
    rear++;
}

// 큐 제거
void dequeue(int *x, int *y) {
    *x = queue[front][0];
    *y = queue[front][1];
    front++;
}

// BFS 함수
int bfs(int m, int n) {
    int max_distance = 0;

    while (front < rear) { // 큐가 비어있지 않을 동안
        int x, y;
        dequeue(&x, &y);
        visited[y * m + x] = 1;

        for (int i = 0; i < 4; i++) {
            int nx = x + dir[i][0];
            int ny = y + dir[i][1];

            // 유효 범위 및 방문 여부 확인
            if (nx >= 0 && nx < m && ny >= 0 && ny < n && visited[ny * m + nx] == 0 && graph[ny][nx] == 0) {
                visited[ny * m + nx] = 1; // 방문 처리
                graph[ny][nx] = graph[y][x] + 1; // 거리 갱신
                enqueue(nx, ny);
                if (graph[ny][nx] > max_distance) {
                    max_distance = graph[ny][nx];
                }
            }
        }
    }
    if (max_distance == 0){return 0;} else{
        return max_distance - 1; // 시작점을 포함하므로 1을 뺌
    }
}

int main() {
    int M, N;
    scanf("%d %d", &M, &N);

    // 그래프 입력
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            scanf("%d", &graph[i][j]);
            visited[i * M + j] = 0; // 방문 초기화
            if(graph[i][j] == 1){
                enqueue(j, i);
            }
        }
    }

    // BFS 실행 및 결과 계산
    int max = 0;
    max = bfs(M, N);

    // 0이면서 방문되지 않은 노드가 있으면 -1 출력
    int flag = 0;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            if (graph[i][j] == 0 && visited[i * M + j] == 0) {
                flag = 1;
                break;
            }
        }
        if (flag == 1) break;
    }

    if (flag == 1) {
        
        printf("-1");
    } else {
        printf("%d", max);
    }

    return 0;
}

주요 변수 설명

graph[1000][1000]:
- 상자의 상태를 저장하는 2차원 배열입니다.
- 값 1: 익은 토마토
- 값 0: 익지 않은 토마토
- 값 -1: 비어 있는 칸.
visited[1000000]:
- 방문 여부를 기록하는 배열입니다.
- 값 1: 이미 방문한 좌표.
- 값 0: 방문하지 않은 좌표.
queue[1000001][2]:
- BFS 탐색에 사용되는 큐로, 익은 토마토의 좌표를 저장합니다.
dir[4][2]:
- 상하좌우 탐색 방향을 나타내는 배열입니다.

코드 상세 해설

1. 큐 삽입과 제거

BFS 탐색에서 사용할 큐에 좌표를 삽입하거나 제거하는 함수입니다.

void enqueue(int x, int y) {
    queue[rear][0] = x;
    queue[rear][1] = y;
    rear++;
}

void dequeue(int *x, int *y) {
    *x = queue[front][0];
    *y = queue[front][1];
    front++;
}

2. BFS 함수

이 함수는 BFS 탐색을 수행하여 모든 토마토를 익히는 데 걸리는 최소 시간을 계산합니다.

int bfs(int m, int n) {
    int max_distance = 0;

    while (front < rear) { // 큐가 비어있지 않을 동안
        int x, y;
        dequeue(&x, &y);
        visited[y * m + x] = 1;

        for (int i = 0; i < 4; i++) {
            int nx = x + dir[i][0];
            int ny = y + dir[i][1];

            // 유효 범위 및 방문 여부 확인
            if (nx >= 0 && nx < m && ny >= 0 && ny < n && visited[ny * m + nx] == 0 && graph[ny][nx] == 0) {
                visited[ny * m + nx] = 1; // 방문 처리
                graph[ny][nx] = graph[y][x] + 1; // 거리 갱신
                enqueue(nx, ny);
                if (graph[ny][nx] > max_distance) {
                    max_distance = graph[ny][nx];
                }
            }
        }
    }

    if (max_distance == 0) {
        return 0;
    } else {
        return max_distance - 1; // 시작점을 포함하므로 1을 뺌
    }
}

동작 과정:

초기 상태에서 큐에 익은 토마토(값 1)의 좌표를 삽입하고 BFS 탐색 시작.
큐에서 좌표를 하나씩 꺼내며 상하좌우 방향으로 탐색.
유효한 범위 내에서 익지 않은 토마토(값 0)를 찾으면:
- 방문 여부를 기록(visited).
- graph 배열에 현재 거리(일수)를 갱신(graph[y][x] + 1).
- 새 좌표를 큐에 삽입.
모든 토마토를 익히는 데 걸린 최장 거리(max_distance)를 계산.

3. 입력 및 초기화

상자의 상태를 입력받아 graph에 저장하고, 익은 토마토(값 1)의 좌표를 큐에 삽입합니다.
방문 여부(visited)는 모두 0으로 초기화합니다.

for (int i = 0; i < N; i++) {
    for (int j = 0; j < M; j++) {
        scanf("%d", &graph[i][j]);
        visited[i * M + j] = 0; // 방문 초기화
        if (graph[i][j] == 1) {
            enqueue(j, i); // 익은 토마토 큐에 삽입
        }
    }
}

4. 결과 계산

BFS 탐색 후, graph 배열에서 값 0이 남아 있으면 익히지 못한 토마토가 존재하는 것입니다.

int flag = 0;
for (int i = 0; i < N; i++) {
    for (int j = 0; j < M; j++) {
        if (graph[i][j] == 0 && visited[i * M + j] == 0) {
            flag = 1; // 익히지 못한 토마토 발견
            break;
        }
    }
    if (flag == 1) break;
}

출력:

flag == 1: 익히지 못한 토마토가 있으므로 -1 출력.
flag == 0: 모든 토마토를 익히는 데 걸린 최대 거리(max) 출력.

if (flag == 1) {
    printf("-1");
} else {
    printf("%d", max);
}

시간 및 공간 복잡도

시간 복잡도:

BFS는 각 노드를 한 번만 방문하므로 O(N×M)O(N \times M).

공간 복잡도:

graph, visited, queue 배열을 사용하므로 O(N×M)O(N \times M).

💡 도움이 되셨다면 댓글과 공감 부탁드립니다! 😊
📌 더 많은 알고리즘 풀이와 프로그래밍 자료는 블로그에서 확인하세요!
✉️ 문의나 피드백은 댓글이나 이메일로 남겨주세요.

'Computer Science > 알고리즘 문제' 카테고리의 다른 글

C - [백준 11729] 하노이 탑 이동 순서 (feat. 재귀적 사고) (0)	2024.12.30
C - [백준 4179] 불! (feat. 이중 BFS) (0)	2024.12.29
C - [백준 1926] 그림 (feat. BFS, 연결요소, 방향) (0)	2024.12.27
C - [백준 2178] 미로탐색 (feat. BFS & 최단거리 탐색) (0)	2024.12.26
C - [백준 11724 재구현] 연결 요소의 개수 (feat. 리스트) (0)	2024.12.24