
https://www.acmicpc.net/problem/9663
백준 9663번 - N-Queen 문제
N-Queen 문제는 N×N 체스판 위에 N개의 퀸을 놓는 방법의 수를 찾는 문제입니다. 퀸은 같은 행, 열, 대각선 상에 위치한 다른 퀸을 공격할 수 있으므로, 서로 공격하지 않도록 배치해야 합니다.
입력
- N(1 ≤ N ≤ 15): 체스판의 크기 및 퀸의 개수
출력
- 조건을 만족하는 퀸 배치의 경우의 수
예제 입력 1
8
예제 출력 1
92
Checkpoint
1.
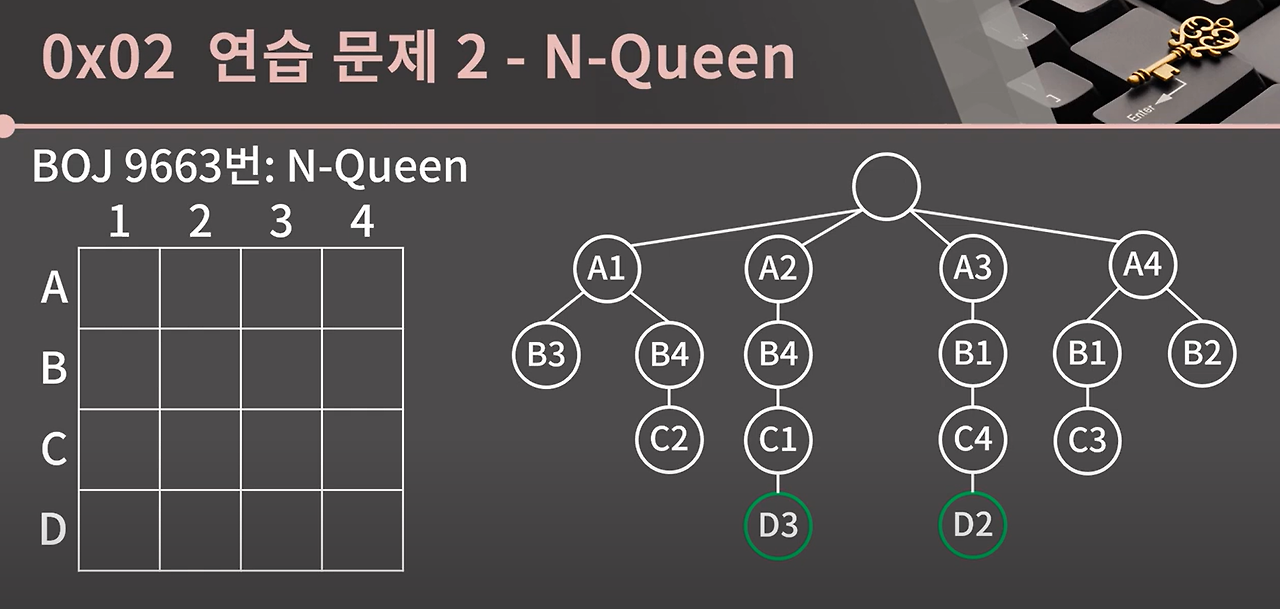
각 행의 퀸은 1개씩 밖에 놓을 수 없기 때문에 첫 행에 퀸을 하나 배치하고 다음 행에 놓을 수 있는 공간에 퀸을 배치하고 그 다음 행에 놓일 수 있는 공간에 퀸을 배치하고 N개 행까지 전부 배치가 된다면 그 경우의 수는 성공이기 때문에 카운트를 하면 된다는 접근이 필요합니다.
2024.12.30 - [Computer Science/자료구조 & 알고리즘] - [자료구조 & 알고리즘] 백트래킹 (feat. DFS, 재귀)
우측의 트리가 "상태공간트리"인데, 직관적으로 보면 각 층(lavel)은 행을 나타내고 있습니다. A1에 퀸을 놓았을 때 두번째 행인 B행에 퀸을 놓을 수 있는 경우의 수 (B3, B4)를 따져보고 세번째 행인 C행에 퀸을 놓을 수 있는 경우의 수를 따지면서 N행(리프노드)까지 도달하는 것이 목표입니다. N행에 도달하는 것이 목표인 이유는 각 행에 퀸을 하나씩 밖에 놓을 수 없기 때문입니다. 즉 N이 4로 주어졌을 경우 A,B,C,D 행에 퀸을 전부 놓을 수 있는 것, 즉 깊이가 리프노드까지 도달할 수 있는 것이 정답이 됩니다.
2.
사실, 이 문제를 푸는 가장 큰 난관이었던 것은, 백트래킹 자체 보다는 퀸을 놓을 수 있는지 없는지 판단하는 것이었습니다.
퀸은 상하좌우 뿐만 아니라 대각선으로도 움직이기 때문에, 이를 어떻게 판단할 것인가 설계하는데 힘들었고 대각선에 대한 판단은 풀이을 보고 이해하였습니다.
"좌우" 에 대해 걱정할 필요는 없었습니다. 이유는 즉슨 각 행에 퀸은 하나씩 밖에 없다는 조건에 입각하여, 한 행(level)을 처리할 때 하나의 퀸만 놓기 때문에 같은 행에 퀸이 2개가 존재할 수 없기 때문입니다.
다시 말하자면, 행을 내려가는 for문, for(int i = 0; i < row; i ++) 이 있다면 이 반복문 한번에 하나의 퀸이 처리되지 for문 안에 퀸의 배치를 2번 하는 경우가 없기 때문에 "좌우"에 대한 판단은 할 필요가 없었습니다.
"상하" 일 경우 열을 비교하면 되었습니다.
for (int prev_row = 0; prev_row < row; prev_row++) {
// 같은 열에 퀸이 있는 경우
if (columns[prev_row] == col)
return 0;
현재의 열, col 과 해당 행전의 퀸의 위치를 저장하고 있는 columns에서 이미 배치한 퀸의 열을 비교하면서 같은 행이 있을 경우, 퀸을 놓을 수 없다고 판단하고 return 0을 함으로서 재귀를 종료시킵니다.
문제는 "대각선" 인데 ,
if (abs(columns[prev_row] - col) == row - prev_row)
이 처럼
행의 차이와 열의 차이가 똑같은 경우 대각선이 있다고 판단합니다.
(수학적 접근이라고 하는데 생각을 못해내어서 모범답안을 확인하였습니다...)
접근 방법
- 백트래킹 활용
- 각 행에 하나의 퀸을 놓는 방식으로 탐색을 진행합니다.
- 유효하지 않은 경우를 만나면 더 이상 탐색하지 않고 이전 상태로 돌아갑니다.
- 유효성 검사
- 같은 열에 퀸이 있는지 확인.
- 두 대각선(좌상단 ↔ 우하단, 우상단 ↔ 좌하단)에 퀸이 있는지 확인.
- 재귀 호출
- 현재 행에 퀸을 배치한 후 다음 행을 탐색합니다.
- 모든 행에 퀸을 배치하면 카운트를 증가시킵니다.
구현코드
#include <stdio.h>
#include <stdlib.h>
int N;
int count = 0;
int *columns;
int is_safe(int row, int col) {
for (int prev_row = 0; prev_row < row; prev_row++) {
// 같은 열에 퀸이 있는 경우
if (columns[prev_row] == col)
return 0;
// 대각선에 퀸이 있는 경우
if (abs(columns[prev_row] - col) == row - prev_row)
return 0;
}
return 1;
}
void place_queen(int row) {
if (row == N) {
count++;
return;
}
for (int col = 0; col < N; col++) {
if (is_safe(row, col)) {
columns[row] = col;
place_queen(row + 1);
}
}
}
int main() {
scanf("%d", &N);
columns = (int *)malloc(sizeof(int) * N);
place_queen(0);
printf("%d\n", count);
free(columns);
return 0;
}
코드 구조
코드는 백트래킹(Backtracking)을 활용하여 가능한 모든 퀸 배치를 시도합니다. 불가능한 배치는 탐색을 중단하고 되돌아갑니다.
- is_safe: 특정 위치에 퀸을 놓을 수 있는지 확인합니다.
- place_queen: 각 행에 퀸을 놓으며 재귀적으로 배치를 진행합니다.
- main: 입력을 받아 초기화하고 백트래킹 함수를 호출하여 결과를 출력합니다.
1. 유효성 검사 함수 is_safe
int is_safe(int row, int col) {
for (int prev_row = 0; prev_row < row; prev_row++) {
if (columns[prev_row] == col)
return 0;
if (abs(columns[prev_row] - col) == row - prev_row)
return 0;
}
return 1;
}
- 같은 열 검사
columns[prev_row] == col: 이전 행에 놓인 퀸이 같은 열에 있다면 배치 불가. - 대각선 검사
abs(columns[prev_row] - col) == row - prev_row: 두 퀸의 열 차이와 행 차이가 같다면 대각선 상에 위치하므로 배치 불가.
2. 백트래킹 함수 place_queen
void place_queen(int row) {
if (row == N) {
count++;
return;
}
for (int col = 0; col < N; col++) {
if (is_safe(row, col)) {
columns[row] = col;
place_queen(row + 1);
}
}
}
- 종료 조건
if (row == N): N개의 퀸을 모두 배치하면 count를 증가시키고 종료합니다. - 열 탐색 및 재귀 호출
for (int col = 0; col < N; col++): 현재 행에서 모든 열을 시도하며, is_safe 함수로 유효성을 확인합니다. 유효하면 퀸을 배치하고 다음 행을 탐색합니다.
3. 메인 함수
int main() {
scanf("%d", &N);
columns = (int *)malloc(sizeof(int) * N);
place_queen(0);
printf("%d\n", count);
free(columns);
return 0;
}
- 입력 및 초기화
scanf("%d", &N): 체스판 크기를 입력받고, 크기에 맞는 배열을 동적으로 할당합니다. - 결과 출력
printf("%d\n", count): 가능한 배치의 총 개수를 출력합니다. - 메모리 해제
동적으로 할당한 메모리를 사용 후 해제합니다.
💡 도움이 되셨다면 댓글과 공감 부탁드립니다! 😊
📌 더 많은 알고리즘 풀이와 프로그래밍 자료는 블로그에서 확인하세요!
✉️ 문의나 피드백은 댓글이나 이메일로 남겨주세요.
'Computer Science > 알고리즘 문제' 카테고리의 다른 글
| C - [백준 1759] 암호 만들기 (feat. 백트래킹 + DFS) (0) | 2025.01.05 |
|---|---|
| C - [백준 1987] 알파벳 (feat. 백트래킹, DFS & 최장거리 탐색) (0) | 2025.01.05 |
| C - [백준 15649, 15650] N 과 M 시리즈 정복하기 (feat. 백트래킹, 순열) (0) | 2025.01.03 |
| C - [백준 2447] 별 찍기 -10 (feat. 재귀) (0) | 2025.01.02 |
| C - [백준 1992] 쿼드트리 (feat. 재귀) (1) | 2025.01.01 |



