참고 포스트
https://rnasterofmysea.tistory.com/61
[알고리즘] 단순 반복을 넘어서: 절차적 사고에 재귀를 더하다
도입부 (Introduction) : 재귀적 사고의 필요성 여태까지 컴퓨터정보공학을 전공하면서 알고리즘에 대한 공부가 취약했기 때문에 튼튼한 기초를 잡고자 알고리즘의 기초부터 공부하기 시작했습니
rnasterofmysea.tistory.com

https://www.acmicpc.net/problem/2630
문제 설명
백준 2630번: 색종이 만들기는 분할 정복(Divide and Conquer)을 이용하여 문제를 해결하는 방식입니다. 주어진 N×NN \times N 크기의 종이가 흰색(0)과 파란색(1)으로 이루어져 있고, 이를 규칙에 따라 최소 개수의 색종이로 나누는 문제입니다.
규칙
- 주어진 색종이가 모두 같은 색(흰색 또는 파란색)으로 이루어져 있다면, 더 이상 나누지 않고 하나의 색종이로 간주합니다.
- 다른 색이 섞여 있다면, 색종이를 4개의 같은 크기의 정사각형으로 나누어 각 부분을 다시 검사합니다.
- 결과적으로 흰색 색종이와 파란색 색종이의 개수를 출력합니다.
입력
- 첫 번째 줄에 NN (NN은 2의 제곱수, 2≤N≤642 \leq N \leq 64).
- 이후 NN개의 줄에 NN개의 정수(0 또는 1)로 이루어진 색종이 정보가 주어집니다.
출력
- 첫 번째 줄: 흰색 색종이의 개수.
- 두 번째 줄: 파란색 색종이의 개수.

Checkpoint
재귀적 사고
전 포스트( https://rnasterofmysea.tistory.com/61) 에서 언급한 "재귀적 사고"로 알고리즘을 설계하는 방법에 입각하여,
재귀 규칙(recursion case) 정의, 기저조건(base case) 정의를 진행한다.
재귀 규칙:
현재 종이의 색이 단일색이 아니라면, 즉 모두 하얀색(0)이거나 파란색(1)이지 않으면 종이를 4등분 한다.
기저조건:
종이의 크기가 1일 경우 더 나눌 수 없기 때문에 크기가 1인 색종이의 색깔을 판단하여 카운트한다 (재귀 종료 포인트) .
현재 종이가 단일 색이라면 종이의 색깔을 판단하여 카운트하고 해당 종이에 대한 처리를 완료한다(재귀 종료 포인트).
재귀가 종료되면 분할 정복이 완료되었음을 의미하고 문제에서 요구하는 값을 도출한다.
분할정복 관점에서의 알고리즘 설계
- Base Case: 색종이가 모두 같은 색(0 또는 1)이라면 그 색종이 개수를 증가시키고 반환.
- Divide: 색종이가 같은 색으로 이루어져 있지 않다면, 색종이를 4등분하여 각각 재귀 호출.
- Conquer: 모든 분할이 끝나면 결과를 합산.
구현 코드 (C)
/*
BOJ_2630_색종이 만들기
https://www.acmicpc.net/problem/2630
*/
#include <stdio.h>
#define MAX 128;
int paper[128][128];
int white_count = 0;
int blue_count = 0;
void count(int color){
if(color){
blue_count++;
} else{
white_count++;
}
};
void recursion(int x, int y, int size){
// 종료조건(base case)
if(size == 1){
count(paper[x][y]);
return;
}
//재귀조건(recursion case)
int current = paper[x][y];
int temp = 0;
for(int i = x; i < x + size; i++){
for(int j = y; j < y + size; j++){
if(paper[i][j] == current){
continue;
} else{
temp = 1;
break;
}
}
if(temp){
break;
}
}
if(temp == 0){
count(current);
return;
} else{
int new_size = size / 2;
for(int i = 0; i < 2; i ++){
for(int j = 0; j < 2; j++){
recursion(x + i * new_size , y + j * new_size, new_size);
}
}
}
}
int main() {
int N = 0;
scanf("%d", &N);
for(int i = 0; i < N; i ++){
for(int j = 0 ; j < N; j ++){
scanf("%d", &paper[i][j]);
}
}
recursion(0, 0,N);
printf("%d\n", white_count);
printf("%d\n", blue_count);
return 0;
}
주요 구성 요소 및 해설
1. 전역 변수
int paper[128][128];
int white_count = 0;
int blue_count = 0;
- paper: N×N 크기의 색종이 정보를 저장하는 배열.
- white_count: 흰색 색종이의 개수를 저장.
- blue_count: 파란색 색종이의 개수를 저장.
2. count 함수
void count(int color){
if(color){
blue_count++;
} else{
white_count++;
}
};
- 색종이의 색(color)이 흰색(0)인지 파란색(1)인지 판단하여 각각의 개수를 증가시키는 함수.
3. recursion 함수
void recursion(int x, int y, int size){
// 종료조건(base case)
if(size == 1){
count(paper[x][y]);
return;
}
- Base Case:
- 색종이의 크기가 1인 경우, 해당 색종이의 색을 판단하여 개수를 증가시키고 종료합니다.
//재귀조건(recursion case)
int current = paper[x][y];
int temp = 0;
for(int i = x; i < x + size; i++){
for(int j = y; j < y + size; j++){
if(paper[i][j] == current){
continue;
} else{
temp = 1;
break;
}
}
if(temp){
break;
}
}
- 색종이 검증:
- size×size 크기의 색종이가 모두 같은 색인지 확인.
- current에 색종이의 첫 번째 값(paper[x][y])을 저장하고, 모든 칸이 동일한지 검사합니다.
- temp = 1로 설정되면 색종이 내에 다른 색이 섞여 있음을 의미합니다.
if(temp == 0){
count(current);
return;
} else{
int new_size = size / 2;
for(int i = 0; i < 2; i ++){
for(int j = 0; j < 2; j++){
recursion(x + i * new_size , y + j * new_size, new_size);
}
}
}
}
- 분할:
- 색종이에 다른 색이 섞여 있다면, 4개의 하위 색종이로 나누어 재귀 호출.
- 각 색종이의 시작 좌표를 (x + i * new_size, y + j * new_size)로 계산.
4. main 함수
int main() {
int N = 0;
scanf("%d", &N);
for(int i = 0; i < N; i ++){
for(int j = 0 ; j < N; j ++){
scanf("%d", &paper[i][j]);
}
}
recursion(0, 0,N);
printf("%d\n", white_count);
printf("%d\n", blue_count);
return 0;
}
- 입력:
- 색종이의 크기 N과 색종이 정보를 입력받습니다.
- 재귀 호출:
- recursion(0, 0, N)을 호출하여 N×N 크기의 색종이를 탐색합니다.
- 결과 출력:
- 최종적으로 흰색(white_count)과 파란색(blue_count) 색종이의 개수를 출력합니다.
코드 실행 흐름
1. 초기 입력 처리
입력 형식:
- 첫 번째 줄에 색종이 크기 N (N은 2^k, 2≤N≤128).
- 이후 N×N크기의 색종이 정보가 주어짐.
- 각 칸은 0 (흰색) 또는 1 (파란색)으로 구성됨.
예제 입력:
8
1 1 0 0 0 0 1 1
1 1 0 0 0 0 1 1
0 0 0 0 1 1 0 0
0 0 0 0 1 1 0 0
1 0 0 0 1 1 1 1
0 1 0 0 1 1 1 1
0 0 1 1 1 1 1 1
0 0 1 1 1 1 1 1
동작:
- scanf로 NN과 색종이 정보를 입력받아 paper 배열에 저장.
- paper[i][j]는 ii-번째 행, jj-번째 열의 색종이 색을 나타냄.
2. 분할 정복(Divide and Conquer)
전체 영역 처리 순서:
(1) 색종이의 색 일치 확인
- 탐색 범위에서 모든 색이 동일한지 확인.
- current = paper[x][y]로 기준값을 설정하고, 모든 색이 current와 동일한지 검사.
(2) 같은 색인 경우
- 전체가 같은 색이라면 해당 색의 개수 증가.
count(current); // 흰색(0)이면 white_count++, 파란색(1)이면 blue_count++- 탐색 종료.
(3) 다른 색이 섞여 있는 경우
- 색종이를 4등분하여 각 영역에 대해 재귀적으로 recursion 호출.
예제 수행 흐름:
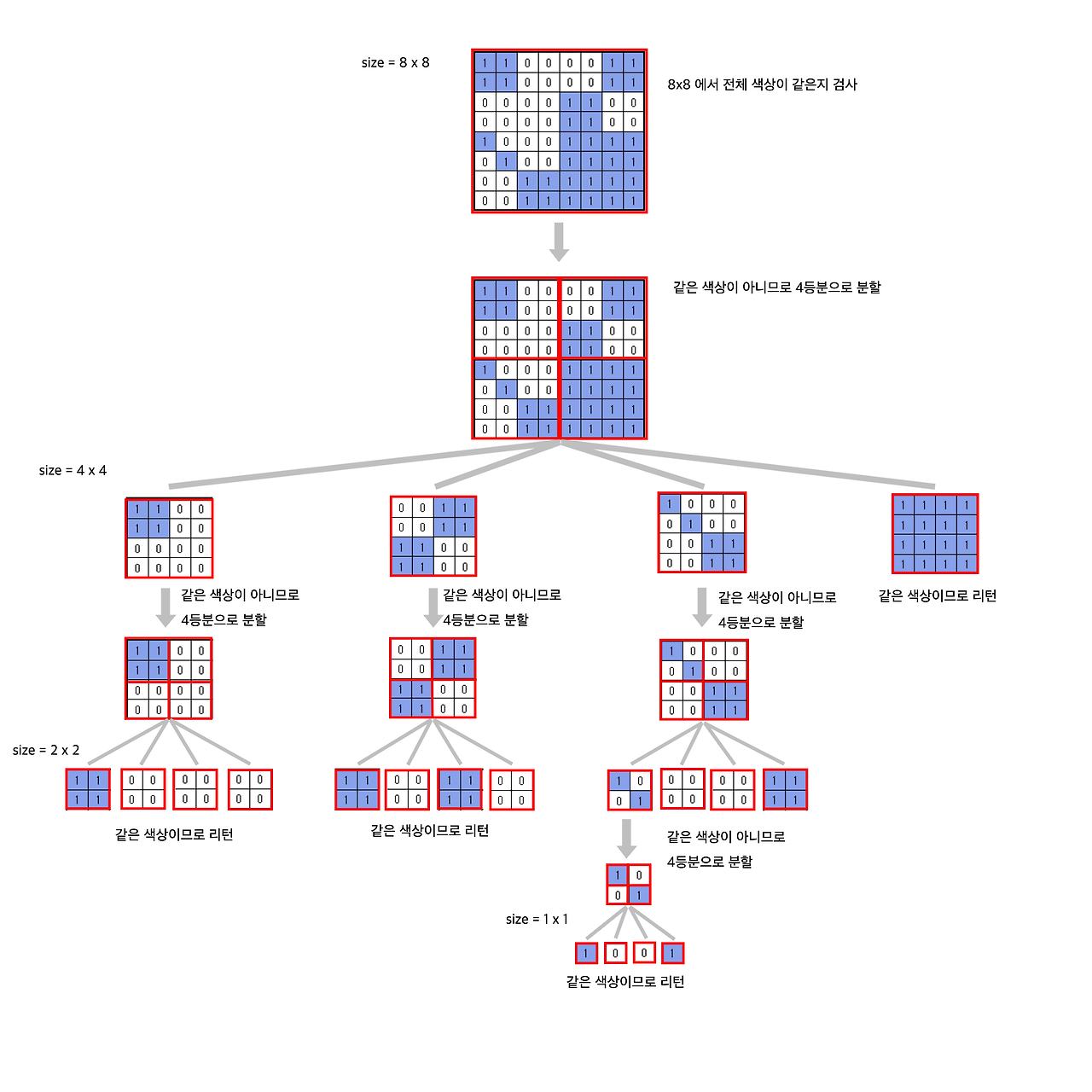
초기 상태:
- 전체 8×8 색종이를 확인:
1 1 0 0 | 0 0 1 1 1 1 0 0 | 0 0 1 1 --------+-------- 0 0 0 0 | 1 1 0 0 0 0 0 0 | 1 1 0 0- 섞인 색이므로 4개의 4×4 영역으로 나눔.
첫 번째 영역 (4×44 \times 4, 좌상단):
1 1 0 0
1 1 0 0
0 0 0 0
0 0 0 0
- 섞인 색이므로 다시 4개의 2×22 \times 2 영역으로 나눔.
첫 번째 하위 영역 (2×2, 좌상단):
1 1
1 1
- 모두 파란색(1) → blue_count++.
두 번째 하위 영역 (2×2, 우상단):
0 0
0 0
- 모두 흰색(0) → white_count++.
나머지 영역도 같은 방식으로 처리.
3. 결과 출력
마지막 결과:
모든 재귀 호출이 종료되면, 각 색종이의 개수를 출력.
예제 출력:
9
7
- 흰색 색종이: 9개.
- 파란색 색종이: 7개.
예제 실행
입력
8
1 1 0 0 0 0 1 1
1 1 0 0 0 0 1 1
0 0 0 0 1 1 0 0
0 0 0 0 1 1 0 0
1 0 0 0 1 1 1 1
0 1 0 0 1 1 1 1
0 0 1 1 1 1 1 1
0 0 1 1 1 1 1 1출력
9
7
시간 및 공간 복잡도
- 시간 복잡도: O(N2logN)O(N^2 \log N)
- N2N^2: 전체 색종이의 모든 칸을 확인.
- logN\log N: 분할 정복의 깊이.
- 공간 복잡도: O(N2)O(N^2)
- 색종이 배열을 저장하는 데 사용.
주요 포인트
- 분할 정복 기법:
- 큰 문제를 작은 문제로 나누고, 작은 문제의 해를 결합하여 큰 문제를 해결.
- 재귀적 사고:
- 문제를 하위 문제로 분할하여 해결하는 과정.
- 종료 조건(Base Case)와 재귀 조건(Recursion Case)의 명확한 설정.
💡 도움이 되셨다면 댓글과 공감 부탁드립니다! 😊
📌 더 많은 알고리즘 풀이와 프로그래밍 자료는 블로그에서 확인하세요!
✉️ 문의나 피드백은 댓글이나 이메일로 남겨주세요.
'Computer Science > 알고리즘 문제' 카테고리의 다른 글
| C - [백준 1992] 쿼드트리 (feat. 재귀) (1) | 2025.01.01 |
|---|---|
| C - [백준1074] Z (feat. 재귀적 사고, 분할정복) (2) | 2024.12.31 |
| C - [백준 11729] 하노이 탑 이동 순서 (feat. 재귀적 사고) (0) | 2024.12.30 |
| C - [백준 4179] 불! (feat. 이중 BFS) (0) | 2024.12.29 |
| C - [백준 7576] 토마토 (feat. BFS, 연결요소, 최단거리) (0) | 2024.12.28 |



